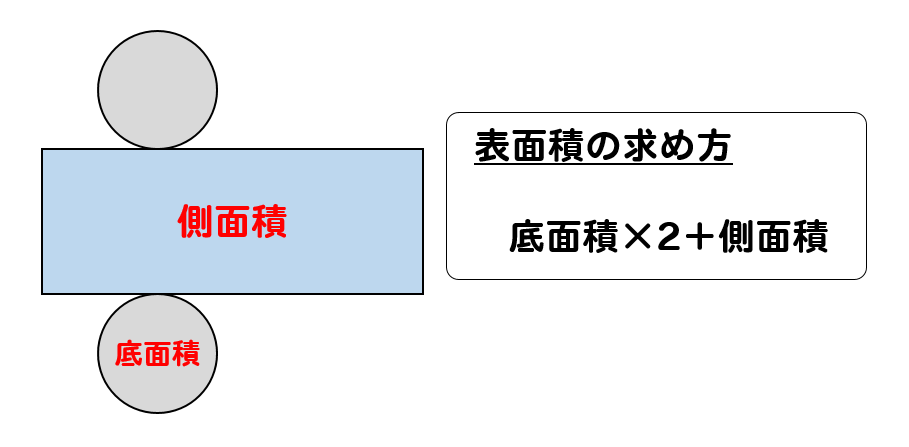
2角柱と円柱 角柱・円柱の体積=底面積×高さ 角柱・円柱の表面積=底面積×2側面積 3角すいと円すいも底面と同じく、面積は π r 2 です。『球と円柱について』(ギリシア語 Περὶ σφαίρας καὶ κυλίνδρου )は、紀元前225年ごろアルキメデスにより発表された2巻からなる著作 。 最も注目すべきは、球面の表面積や球体の体積、円柱のそれにあたる値を見つけ出す方法が詳しく書かれていることであり、アルキメデスはこれ

角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学
円柱 側面積の公式
円柱 側面積の公式-右図イの四角柱の表面積 底面:3×4=12(cm 2)の長方形が2つ 側面:5×4=(cm 2)の長方形が2つ 側面:5×3=15(cm 2)の長方形が2つ 計94(cm 2)・・・答 図ウの円柱の表面積 ウ 底面: π ×2 2 =4 π (cm 2)の円が2つ 側面:底面の円周の長さと側面の横の長さが等しいから 5×4 π = π (cm 2)の長方(面積の復習) a≦x≦b の区間で x 軸と y=f(x) とで囲まれる図形の面積が,縦の長さ f(x) の積分で表された事情を振り返ってみます. a から x までに描かれる図形の面積を S(x) とおくと x がわずかに ⊿x だけ増加したとき,増える面積は黄色で示した長方形の面積,すなわち縦の長さ f(x) と横の




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
円柱側面積公式, 円錐・円柱の体積,側面積 よって、円錐台の側面積は S =πm1Rπm1r =πm1(Rr) で求まる。 一般的に、hの母線の長さをmとすれば S =πm(Rr) (8) となる。 l h R m H l h R m1 m2 r 円柱の底面の形状は「円」なので、底面積は円の面積を計算します。π × ( r1 r2 )× √ ( ( r1 r2 ) × ( r1 r2 ) 高さ × 高さ ) π × ( r1 × r1 r2 × r2 ) で求めることができます。 底面半径 (r1) : 上面半径 (r2) : 高さ (h) : 表面積 : 円錐台の体積 円錐台の表面積 円錐台の側面積 使用しているスクリプトの特性から、特に表面積の証明 半径 の球に内接する円柱の側面積と球の表面積が等しいことを証明します。そうすれば、 と導出できます。まず、球と円柱を高さ方向へ細かくスライスする状況をイメージしてください。 このスライスしたところの面積は 円柱: 球:
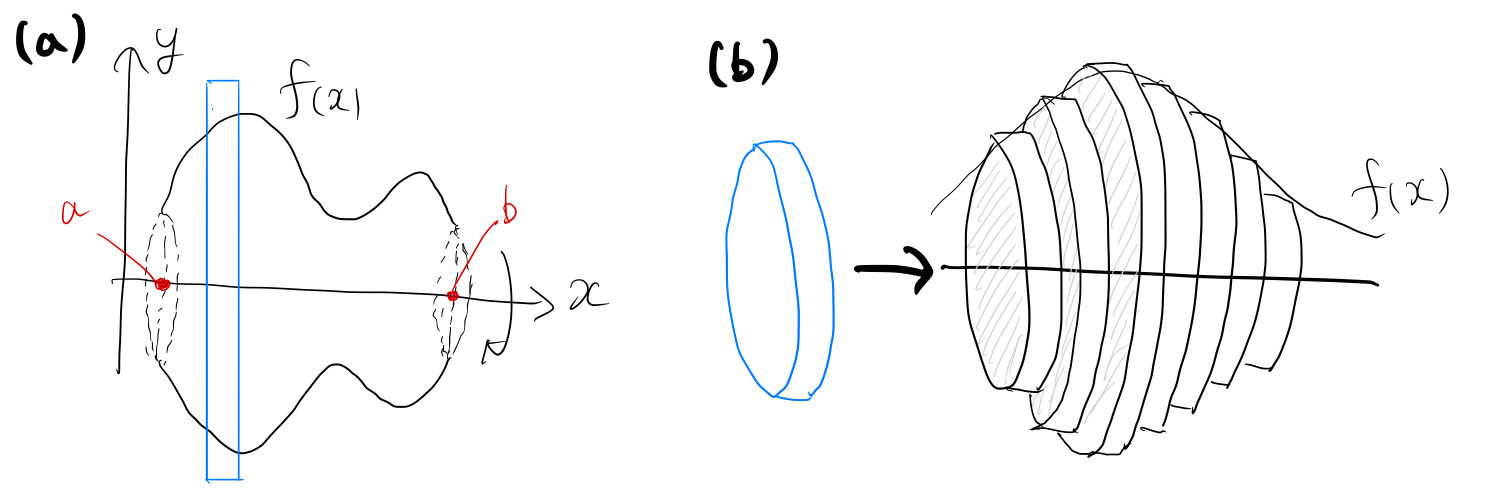
も円柱の側面積の積み重ねの考え方が適用できるのか. (C) 回転体の体積を求めるときに,円錐台の体積の積み重ねで求めてもよいか.また,円柱 の体積の積み重ねでの考え方とどう違うのか. (D) 回転体の側面積の公式 S f x f x dx b ³ aπ × 直径 × 直径 × 高さ ÷ 4 で求めることができます。 直径 (d) : 高さ (h) : 体積 : π(円周率)= 直円柱の体積 (半径から) 直円柱の表面積 (半径から) 直円柱の側面積 (半径から) 直円柱の体積 (直径から) 直円柱の表面積 (直径から) 直円練習問題で理解を深める! まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! こちらの関連記事はいかがでしょうか?
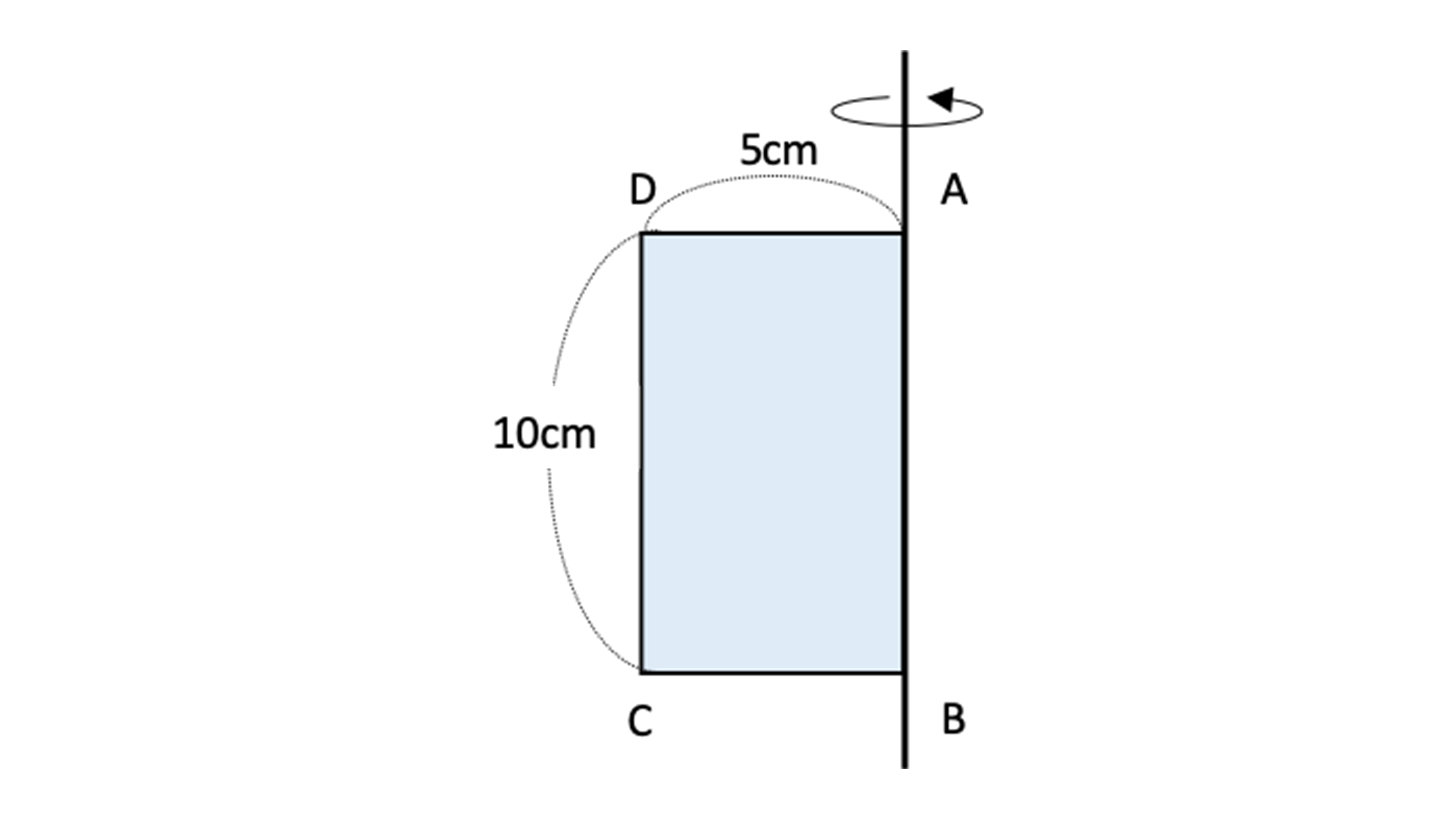
バウムクーヘン積分 タイプ: 入試の標準 レベル: ★★★ 数学Ⅲの積分で, y y 軸周りに回転させる立体の体積の問題があります. 教科書通り y y で積分する方法が正攻法なのですが, x x で (円柱の側面積)を積分する方法がバウムクーヘン 円柱の表面積の求め方公式 円柱の表面積を求めるときには次の公式を使います。 円柱の表面積=底面積×2+ 円柱の側面積 円柱の側面積 =円柱の高さ×底面の円周の長さ なので 円柱の表面積=底面積×2+円柱の高さ×底面の円周の長さ とも書けます。立体の体積および側面積 コンクリートに関する数値表・単位換算表・公式集 1圧縮強度 1圧縮強度 2単位質量 2単位質量 1長さおよび距離 1長さおよび距離 2面積 2面積



円柱の側面積は 1分でわかる求め方 公式 底面積と表面積 体積との関係




公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく
円柱の体積の求め方を確認したところで、円柱の体積の公式についてふれておきましょう。 ある円柱において、底面の円の半径を r 、高さを h 、その円柱の体積を V とすると、V=πr 2 h 体積・表面積の公式や求め方、単位あり計算問題 21年2月19日 この記事では、「円柱」の公式(体積・表面積)や実際の求め方をできるだけわかりやすく解説していきます。 また、リットルなどの単位を含む計算問題なども紹介していきますので、この円柱の表面積の解説 円柱の表面積を求めるには、まず上下の円の部分と側面の部分を分けて考えます。側面部分は筒状ですが、開いて四角形の状態にします。 円の面積は 半径×半径×円周率 なので




角柱 円柱の表面積と体積の公式 数学fun



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
数学トピックQ&A 球の体積にちなんで有名なアルキメデスの話をしましょう。 アルキメデス(Archimedes BC287~212)は,紀元前250年ごろ,地中海のシチリア島にいたギリシャの数学者で,「てこの原理」,や浮力に関する「アルキメデスの原理」などの発見者 続いては展開すると四角形に見えますが、側面積を求めましょう。 四角形と同じく「縦×横」で計算でき、縦は与えられた13cm、横は先に求めた底面の円周と等しいので12π。 2つを掛け合わすと「13×12=156π (cm2)」になります。円柱形のフェルトプランターの容量の確認 そういえばこんな公式でしたね。 3 1038 30歳代 / 主婦 / 非常に役に立った /




空間図形14 円すい台の体積 Youtube




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
面積= πr × 2πr × 1 2 = π2r2 = 314πr2 円柱の底面積をもとめてみよう。 円柱の底面は「円」。 よって、底面積の求め方は、 半径×半径×円周率 になるよね!?? ってことで、例題の円柱の表面積は、 3×3×π = 9π になるね! Step2 円柱の側面積を計算する! つぎは円柱の側面積を計算し 側面積を求める じゃあ、こんな感じの図形で側面積の公式を求めてみよう このままじゃ、何をすればいいのかさっぱりわからないよね だから、展開して考えるよ! 展開するとこうなるね ピンクの部分は、小さい円の円周を求めたよ!
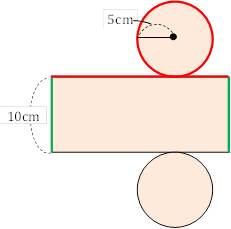



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




円柱の表面積 Youtube
円錐の側面積と中心角を一瞬で求めてしまう裏ワザ公式です! まぁ、受験ではほとんどの人がこの裏ワザ公式を利用することになると思います。 だって、めっちゃくちゃ簡単だから。 そんな裏ワザ公式とは 母線と半径の長さを利用して一般的に、表面積を直感的方法で求めることは、難しい。 (球の表面積が、球に外接する円柱の側面積に等しいことが言えればよい。) それに対して、体積の方は、 カヴァリエリ(Cavalieri)の原理 円錐の表面積の公式を使うのもokですが、ここでは定石通り、底面積と側面積を求めてから円錐の表面積を求めてみます。 まず、 底面積 =3 2 π =9π・・・① ですね。 次に、側面積を求めます。まず、円錐の展開図を考えて、下の図におけるlを求めます。




โน ตของ 体積 表面積 側面積 の公式 ช น Junior Clear




公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく
円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S円がぴったり 入る円柱 円がぴったり 入る円柱 球の直径と等しい長さの半径をもつ円になった 円の面積=π(2r)² (rは球の半径) =4πr² 球の表面積=円柱の側面積→円柱の側面積を求める 具体物での実験をもとに公式を導きます。よって球の表面積は外接円柱側面の面積に等しい、 とう趣旨を主張している。 12 節回転体の体積 任意の面を軸の回わりに回転させた回転体の体積公式は、 西洋流ではバッポス = ギュルダンの公式と呼ばれる。関も、 と (3 において、公式を4) 「体積=面積




空間図形 円柱の側面積の求め方がわかりません 中学数学 定期テスト対策サイト



1
円柱の表面積を求める公式は、次の通りです。 S = 2πr2 2πrh = 2πr(r h) S = 2 π r 2 2 π r h = 2 π r (r h) ここで、S は円柱の表面積、π は円周率、r は底面の円の半径、h は高さを表します。側面積を求める計算をすると,上のグラフの山形部分面積を求めればよく, 45 °では, である。 ところがこれは,もとの円柱で考えると(円柱を横から見た図を考えて),斜めに等分しただけに過ぎないので,平面が円柱の側面を真っ二つに切り分けて




円柱の表面積の求め方 公式と計算例




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学
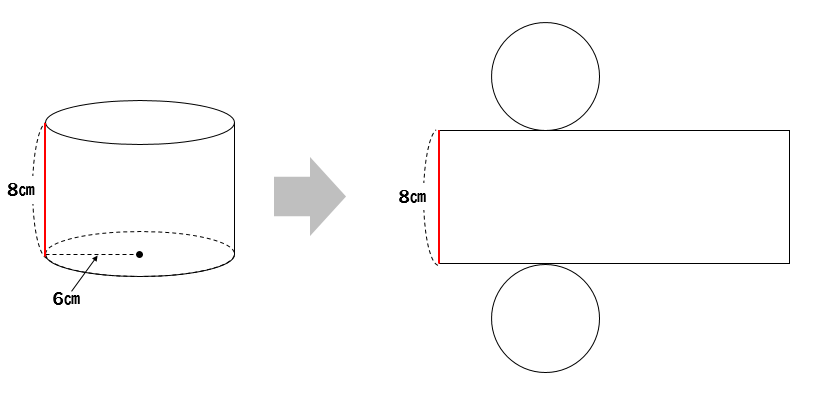



円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ
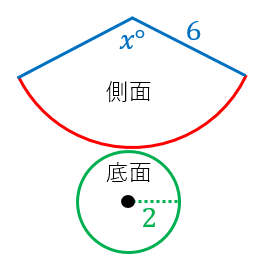



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ



円柱の側面積の求め方を教えてください 円周 高さ円の直径 Yahoo 知恵袋




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン
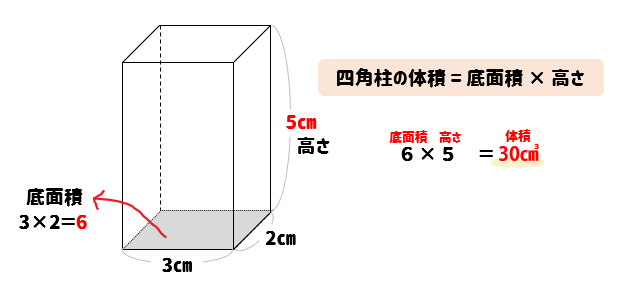



3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学




表面積の求め方 計算公式一覧
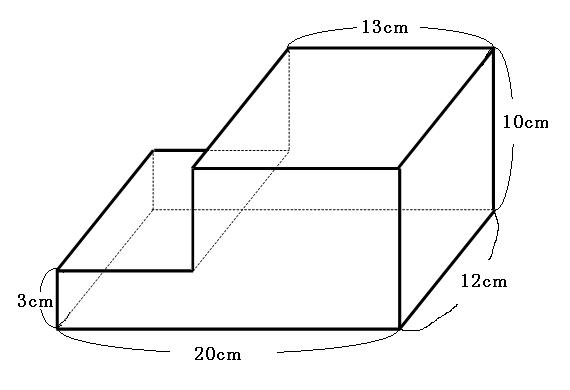



立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか




初等幾何 球の表面積を求める 大人が学び直す数学




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題




円柱




円柱の体積の求め方 公式 小学生 中学生の勉強



算数の問題です 1 図の立体は 円柱を半分に切った形です この立体の体積は何 Yahoo 知恵袋




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu
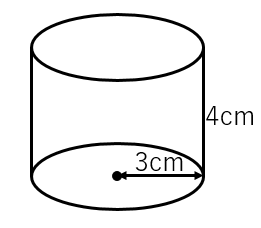



円柱の表面積と体積を求める公式 具体例で学ぶ数学




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学
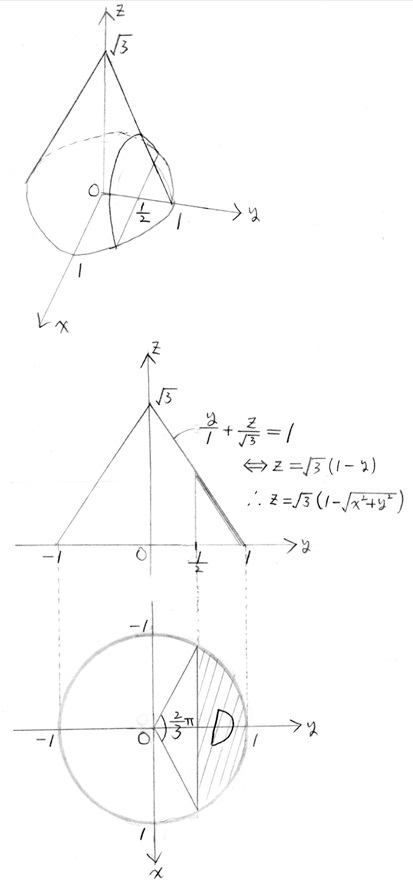



切った円錐 円柱の側面積の求め方 Den Of Hardworking




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット
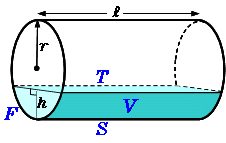



一部が欠けた直円柱の体積 高精度計算サイト




円柱の表面積と体積を求める公式 具体例で学ぶ数学



1




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




角錐 円錐の体積と表面積の公式 数学fun




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく




表面積の求め方 計算公式一覧




円柱の体積の求め方 公式 小学生 中学生の勉強




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun




小6 算数 小6 26 角柱と円柱の体積 基本編 Youtube




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




円柱の表面積の求め方 側面積の考え方をマスターしよう 中学数学 理科の学習まとめサイト
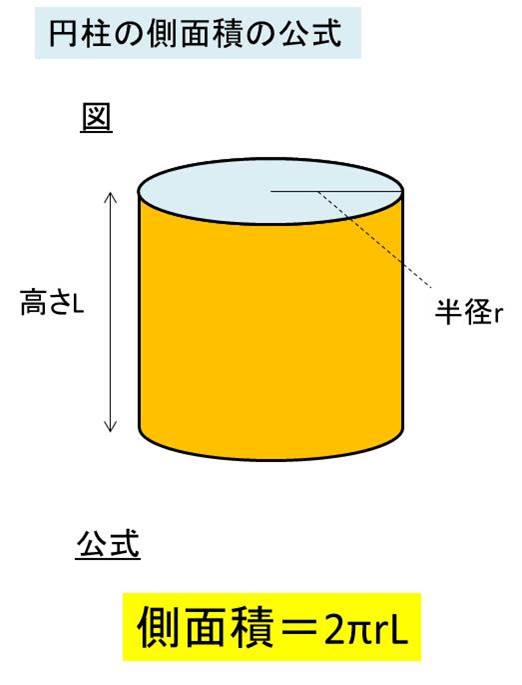



円柱の側面積 底面積 表面積を求める方法 白丸くん
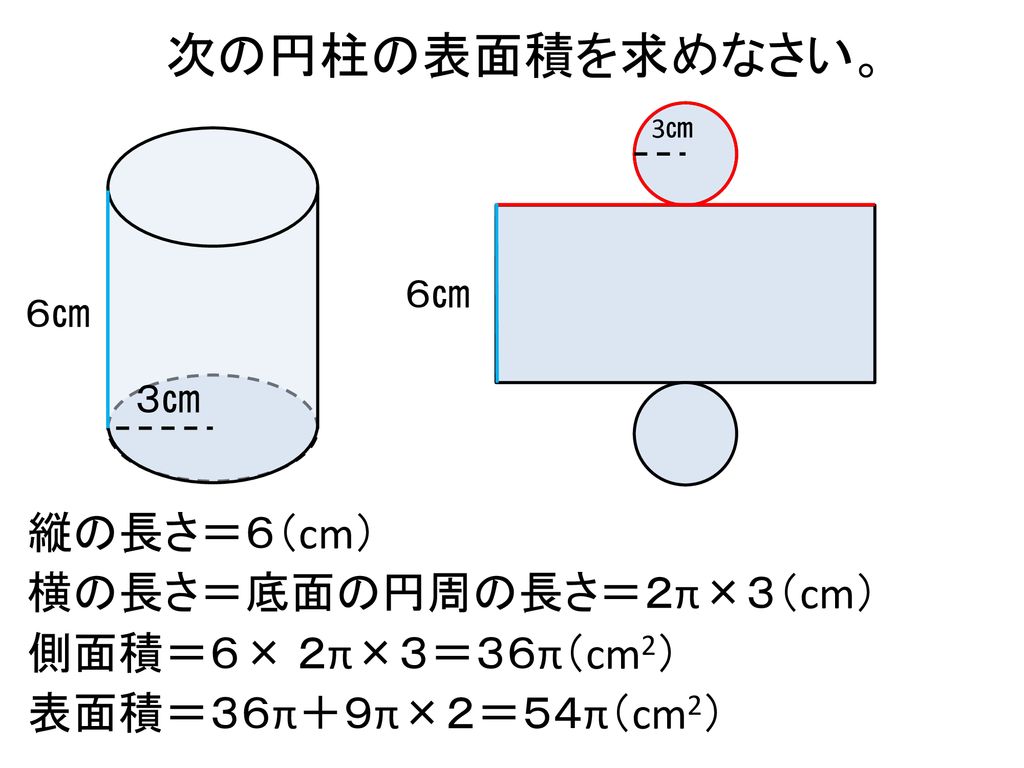



本時の目標 いろいろな立体の表面積を求めることができる Ppt Download



側面 側面積とは 問題を解いて慣れよう 苦手な数学を簡単に




角柱 円柱の表面積と体積の公式 数学fun




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




簡単 円柱の体積公式は底面積 高さ 必ず解きたい計算問題付き 高校生向け受験応援メディア 受験のミカタ




公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく



円柱の側面積は 1分でわかる求め方 公式 底面積と表面積 体積との関係



底面積の求め方は 5分でわかる計算 円柱 円錐 四角柱 三角柱の底面積




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




角錐 円錐の体積と表面積の公式 数学fun




中学数学 円柱の表面積の裏技 使い方と証明 中1数学 Youtube




円柱の表面積の求め方 公式と計算例




円柱を2つ重ねた立体の表面積の求め方 Qikeru 学びを楽しくわかりやすく
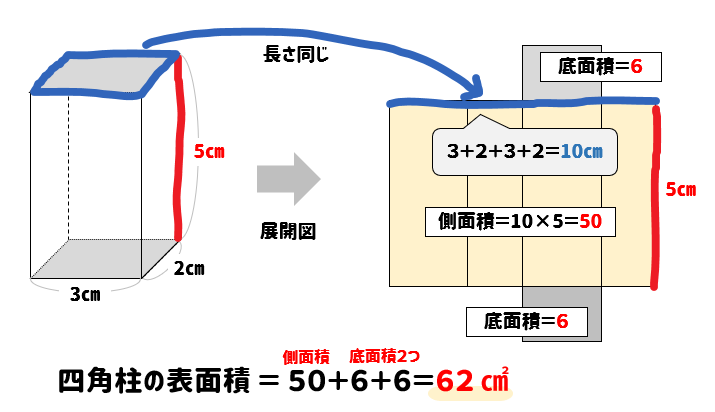



3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ
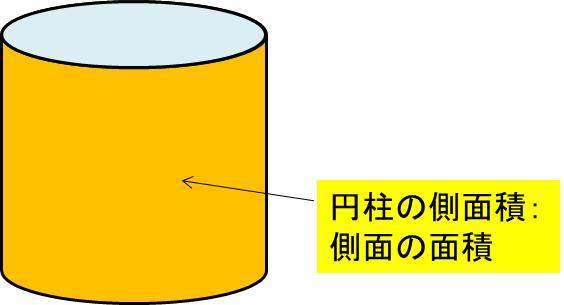



円柱の側面積 底面積 表面積を求める方法 白丸くん




中1 数学 6 2 角柱 円柱の表面積 Youtube




角柱の表面積 Youtube




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学




円柱の体積の求め方 公式と計算例




円柱の表面積 Youtube




公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく
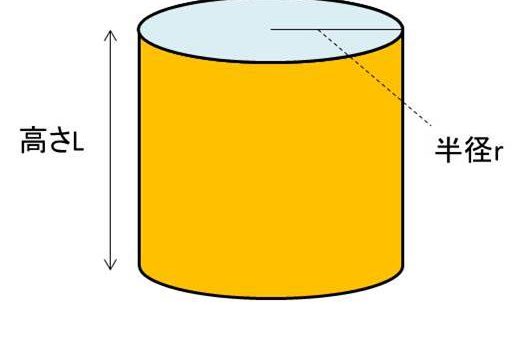



円柱の側面積 底面積 表面積を求める方法 白丸くん




球の表面積と体積の公式 数学fun




円柱の表面積の求め方は ちょっと面倒くさいだけ たぬぬ塾 中学校の先生たち




角柱 円柱の表面積と体積の公式 数学fun




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ



絵でわかる 回転体の側面積 表面積 の求め方 ばたぱら




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学




表面積の求め方 計算公式一覧




角柱 円柱の表面積と体積の公式 数学fun



1
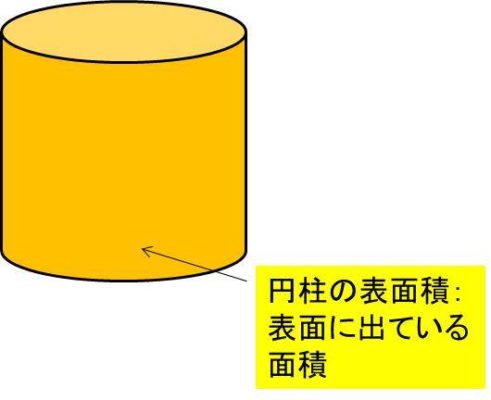



円柱の側面積 底面積 表面積を求める方法 白丸くん




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




簡単 円柱の体積公式は底面積 高さ 必ず解きたい計算問題付き 高校生向け受験応援メディア 受験のミカタ




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




円柱の表面積の求め方の基本 現役塾講師のわかりやすい中学数学の解き方




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




角柱や円柱の表面積の求め方を教えてください Clear




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ



1




円柱の表面積と体積を求める公式 具体例で学ぶ数学



0 件のコメント:
コメントを投稿