パスカルの三角形の作り方、覚え方! 両端に1を書く 間に数を埋める。 完成! パスカルの三角形の使い道 練習問題に挑戦! まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! こちらの関連記事はいかがでしょうか?三角形にはいろんな種類があり、形や大きさは様々です。 しかしどんな三角形でも、 「3 3 つの角の内角をすべて足すと絶対に180° 180 ° になる」 という定理があります。 「図の a a の角度を求めよ」というような問題が出された場合にこれを用います。さて、2項定理でこれらの数が出てくるのが、とっても有名です。 こんなことでしたね。 (a+b) 0 = 1 (a+b) 1 = 1a + 1b (a+b) 2 = 1a 2 + 2ab + 1b 2

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
三角形の定理 小学生
三角形の定理 小学生- 三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。 Step3 ピタゴラスが悩んだ直角二等辺三角形 つぎは、 直角二等辺三角形の辺の長さ を三平方TOP 小学生の算数 図形・面積・体積 練習問題プリント 無料ダウンロード・印刷 小学3年生の算数 三角形正三角形や二等辺三角形 練習問題プリント お気に入り




中学受験算数 等積変形の利用 ヒポクラテスの月
しかし二項定理を三項定理に拡張できるのなら、四項、五項と進めたくなるのが人情です。 そして、最後は「n項定理」という一般系にしてこそ、新しい領域の開拓であり、真の拡張と言えるでしょう。 でも、私は足を止めました。 三角形という「平面」の次に来るのが、三角錐という「立体図形の定義及び性質〔参考:算数教科書の定義・定理辞典 著 志水廣 啓林館わくわく算数〕 図形 定義 性質 三角形 3本の直線で囲まれた図形 角が3つある。 角の総和は180°である。 四角形 4本の直線で囲まれた図形 角が4つある。 角の総和は360°である。 対角線が2本ある。 長方形 すべての角が 三角形の内角の和=180° 小学生女の子 正三角形の1つの角の大きさが60°で角は3つだから 60×3=180だね。 三角定規はどうだったかな。 角のせいしつ 三角定規 検索 三角定規(直角二等辺三角形):45°・45°・90° 三角定規(直角三角形):30°・60°・90°
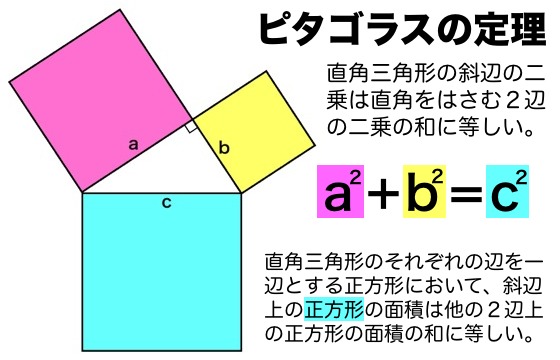
初等幾何学 における ピタゴラスの定理( ピタゴラスのていり 、 英 Pythagorean theorem )は、 直角三角形 の3 辺 の長さの関係を表す。 斜辺 の長さを c, 他の2辺の長さを a, b とすると、定理は が成り立つという 等式 の形で述べられる 。三角形の五心と頂点までの距離 正多面体が5種類しかないことの2通りの証明 cosxの微分公式のいろいろな証明 円周率の求め方(いろいろな計算式) 接弦定理とその逆の証明など 整数部分と小数部分の意味と例題 高校数学の美しい物語 ヒポクラテスの二等辺三角形の定理 二等辺三角形の底角は等しい。 ↓クリック! 二等辺三角形の頂角の二等分線は底辺を 垂直にニ等分する。 ↓クリック! 二等辺三角形がどんな性質をもっているかはよくわかったか な?? 今度は普通の三角形を見て「これは二等辺三角形だ!!」と 見分けられるように
小学生はピタゴラスの定理 (三平方の定理)までは習わなくても、底辺 (または高さ)高さ (または底辺)斜辺=345の整数比になる直角三角形、かつ、斜辺底辺=21になる直角三角形 (正三角形を高さで半分にしたもの)は習う。 図からは斜辺の長さは不明なので S 1 = ( a b) 2 また、 a b c の面積 S 2 は、 S 2 = a b 2 真ん中の 正方形の面積 S 3 は、 S 3 = c 2 大きな正方形 S 1 は、三角形 S 2 4つと 真ん中の正方形 S 3 との合計でも求めることが出来ます。 S 1 = 4 S 2 S 3 ( a b) 2 = 4 × a b 2 c 2 a 2 2 a b b 2 = 2 a b c 2 ∴ a 2 b 2 = c 2 よって、ピタゴラゴラスの定理 a 2 b 2 = c 2 が導き出されました。三平方の定理、小学生バージョンの解き方(江戸川女子中 09年) 図のように、1辺17cmの正方形から同じ形の直角三角形を4つ切り取ってできる正方形の1辺の長さは何cmですか。 2通りの解法例 スマートホンアプリ「立方体の切り口はどんな形? 」 (ネット環境でのFlashアニメーション) スマホ向け解法集




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




中学受験算数 等積変形の利用 ヒポクラテスの月
三角形の計算 ・ 正三角形 (辺から高さと面積) 正三角形の1辺の長さから高さと面積を計算します。 ・ 正三角形 (高さから辺と面積) 正三角形の高さから1辺の長さと面積を計算します。 ・ 正三角形 (面積から辺と高さ) 正三角形の面積から1辺の長さと高さを計算します。 ・ 直角三角形 (底辺と高さ) 直角三角形の底辺と高さから、斜辺と角度と面積を計算します 今回は「直角三角形TOP7」と題して、三平方の定理にまつわるお話をしていきます。 三平方の定理は、直角三角形の斜辺の2乗が他の辺の2乗の和に等しい、という公式です。 非常に便利ですが、二次方程式になってしまうので解答するのに時間がかかります。 そこで、テストによく出てくる直角三角形については暗記してしまいましょう。 ここでは、特に 直角三角形とは? 定義や定理、辺の長さの比、合同条件 21年2月19日 この記事では、「直角三角形」の定義や合同条件、重要な辺の長さの比について解説していきます。 また証明問題もわかりやすく説明していくので、ぜひマスターしてくださいね




応用力 二等辺三角形の面積 小学生対応 2
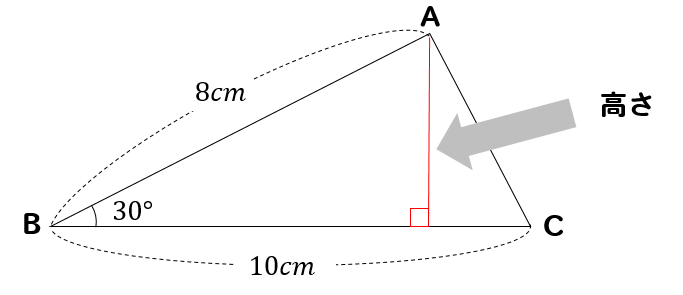



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ
ただ、三角形の成立条件を理解するためには、「 2 2 つの円の位置関係 」と結び付けるのが最適です。 少し大きいですが図をご覧ください。 a > b c a > b c 、 a = b c a = b c のときは三角形が作れず、 a < b c a < b c のときは三角形が作れましたね。 本記事では、このロジックを大切に話を進めますよ。 今、 a a を最大の辺としましたが、 b b が最大、 c c が最大の まとめ:直角三角形の比3つを使い倒せ! 中学数学でよく使う直角三角形の比は次の3つ。 30、60の直角三角形 45の直角三角形 3 4 5の直角三角形 これを覚えるだけで三平方の定理を使わなくてよくなるから、 だいぶラクになるね。 いきなり覚えるのは 二等辺三角形の定理「二等辺三角形の底角は等しい」から、ポイントは二等辺三角形の底角を見つけることです。 ⑴は、1つの底角の大きさが62°なので、もう1つの底角の大きさも62°です。三角形の内角の和が180°(定理)なので、 X=180°−2×62°=56° ⑵は、頂角が直角で、底角の大き
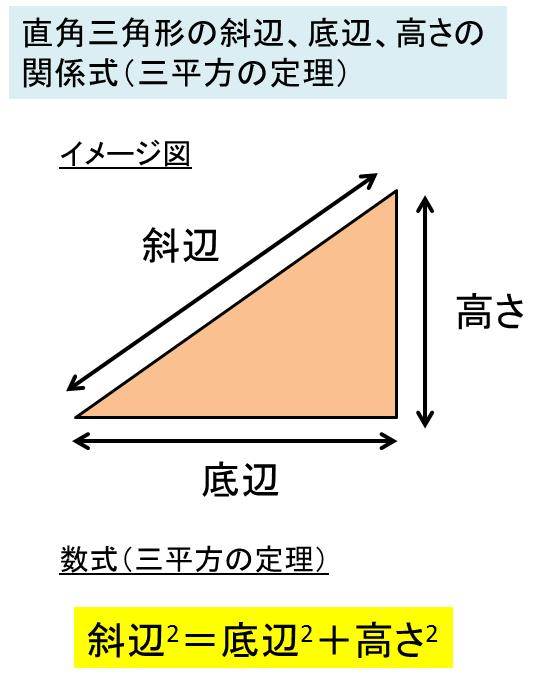



Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 直角三角形の辺の求め方




中学受験算数で三平方の定理は使っていいのか ワイズナビ
小学生の基礎から始めよう 三角比(30°,45°,60°) 直角三角形の左端の角度が45度(直角二等辺三角形)の時の比率は次のようになります。 1対1対√2(いったいいったいルートに) (底辺a=1、対辺b=1、斜辺c=√2) 1対2対√3と1対1対√2を呪文のように何回でも比率を唱えていれば覚えられ2つの角が等しい三角形は、その 角を底角とする二等辺三角形 定義 長方形 4つの角がすべて等しい四角形 正三角形 定義3つの辺が等しい三角形 長方形の 対角線は等しい 正三角形の3つの角は等しい ひし形 定義4つの辺がすべて等しい四角形 直角三角形2つの三角形に分けて考えていきましょう。 上の緑三角形は底辺が5㎝、高さが4㎝だから $$5\times 4\div2=10(cm^2)$$ 下の黄三角形は底辺が5㎝、高さが2㎝だから $$5\times 2\div2=5(cm^2)$$ 以上より、四角形の面積は $$\Large{105=15(cm^2)}$$ となりました。 面積応用問題




メネラウスの定理が5分でわかる 証明や使い方をイラスト入りで詳しく解説




ピタゴラスの定理の証明に挑戦する小学生 モンテッソーリ教育 ピタゴラスの定理 モンテッソーリ教育 モンテッソーリ
三角形(さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。 その3点を三角形の頂点、3つの線分を三角形の辺という。三角形ADCと三角形AD'Cも同様に底辺と高さが等しいため、面積は等しくなります。という事は、はじめの図形とこの形を変えた図形の面積は等しいという事になりますね。 この形ならば底辺も高さもわかります。底辺12cmで高さ6cmの三角形です。 (式) 12×6÷2 底辺が6cm、高さが3cm。三角形の面積は底辺×高さ÷2で出せる。このとき底辺か高さのどちらかの長さが偶数だと嬉しい。さて二等辺三角形の面積は 6×3÷2=9(cm²) よって赤い部分の面積は 942-9=042(cm²) となる。わかったかな? わからなくても問題はない。なぜなら我々はもう小学生じゃないから。なんの引け目も感じる必要はないのだ。




数学 中3 61 三平方の定理 基本編 Youtube



Math 90 30 60 の直角三角形 辺の長さで成り立つこと 働きアリ
円に関する定理を集めてみた。五角形と円、六角形と円・・・ ここには何か関連がありそう。4点以上が円周上にあることの不思議。 ・・・ やってみてわかってきたこと (1)二つの円で偶数個の円を描くとぴったり一致すること (2)偶数個の円の中心は楕円の外接多角形であること (3)その楕円の焦三角形の内角の和、外角の定理、直角三角形に関する問題です。A03、A04、A08を読んでから取り組んで下さい。 AngleStr3Spdf へのリンク 解答です。 AngleStr3SApdf へのリンク 初級トレーニング4 初級トレーニング最後のプリントです。二等辺三角形 直角三角形 特殊な三角形の代表例としては、他にも正三角形があります。 すべての辺の長さと角度が同じである三角形が正三角形です。 正三角形については、非常に単純な性質を有しています。 一方で二等辺三角形と直角三角形は、正三角形に比べて覚えなければいけない性質が多くなります。 また二等辺三角形と直角三角形は複合問題として



3




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
3年算数「三角形」の教え方をわかりやすく紹介するサイトです。保護者の方や学習支援ボランティアの方々の参考になれば幸いです。 3年算数 三角形 子どもの学習支援 by いっちに算数 スマホ版 ① 三角形の仲間分け ② 二等辺三角形・正三角形の理解 ③ コンパス・定規を使っての二等辺三角 一方メネラウスの定理であれば、トレーニングを積むことで15秒あれば解けるようになります。 前回の記事 ⇒ 三角錐の体積比を楽に求められる公式 次の記事 ⇒ 正三角形の高さと面積は5秒三角形の外角の定理 『外角は、その外角のとなり以外の2つの内角の和に等しい』 つまり、下の図の通り。 外角の定理のひみつ外角= + ①三角形の内角の和は180度でした。 だから、




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学
小学2年生の算数「三角形と四角形」の練習問題プリントです。 三角形と四角形(直角三角形・正方形・長方形・辺・頂点・直角等)の概念を理解し、形の弁別の練習や作図の問題を通して理解を深めることができます。 (プリント12枚) 小学3年生の算数 図形 練習問題プリント 小学3年生の 直角三角形をなす3辺のうち、2辺の長さを知ることができれば、残り1辺の長さを知ることができるというものです。 公式:a² b² = c² 例えば、斜辺5cm、底辺3cmの直角三角形の場合、以下のようにもう1辺の長さを導き出せます。
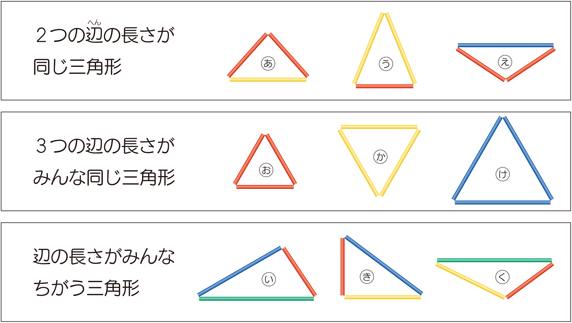



二等辺三角形と正三角形 算数用語集




平面図形をマスター 三角形の面積比 応用編その3




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




世界一わかりやすい数学問題集中3 7章 三平方の定理




小5 算数 小5 31 三角形の角 Youtube




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




平面図形をマスター 三角形の面積比 応用編その3




エレガント直角 三角形 の 定理 最高のカラーリングのアイデア



今 二等辺三角形が熱い 小学校の算数が懐かしい デイリーポータルz



Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau



35 小学生の算数から考える 物理備忘録 津江研究室別館 宇宙見物 科学を通して世界を眺める




二等辺三角形と正三角形 算数用語集



ピタゴラスの定理 小学生バージョン 算数解法の極意




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube
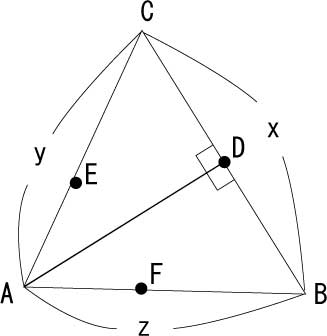



コレクション 三角形 辺の長さ 求め方 小学生 シモネタ




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座



Math 90 30 60 の直角三角形 辺の長さで成り立つこと 働きアリ




直角三角形の辺の長さ 合同条件 面積について アタリマエ



これなら小学生でも分かる 水で車輪を使って ピタゴラスの定理 を証明する実験動画 コモンポストムービー
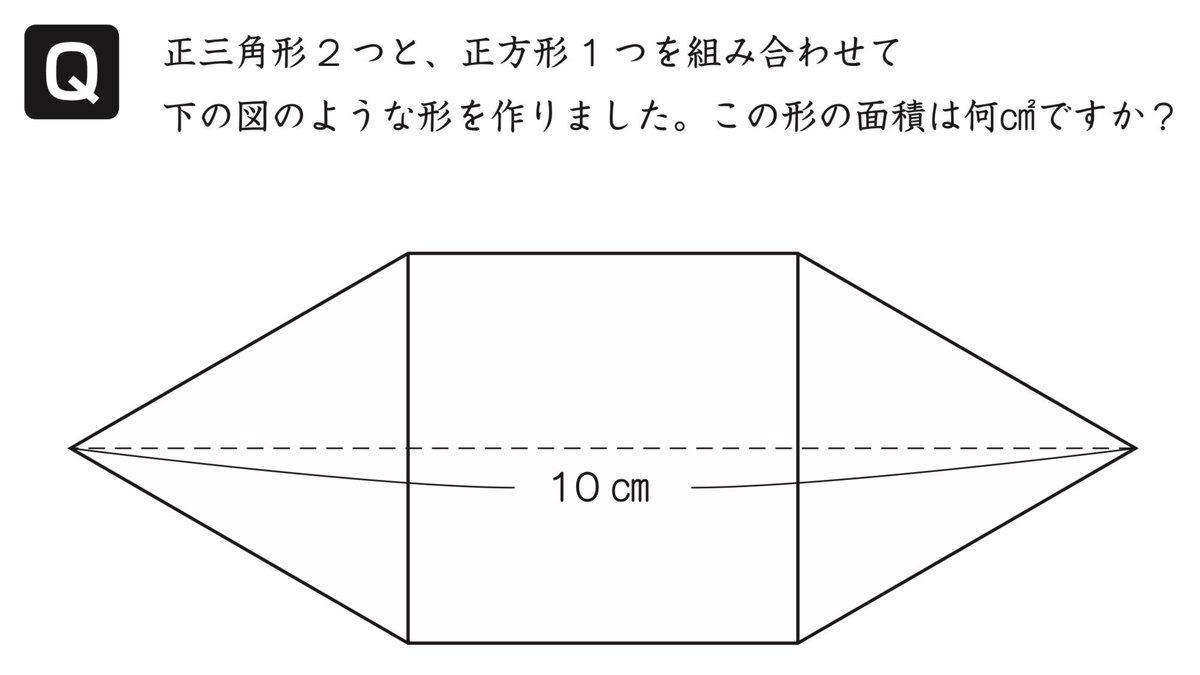



小学校で習う知識だけで解けます ルートも使いません 東大生が小3のときに作った算数の問題 Togetter




直角三角形の辺の長さ 合同条件 面積について アタリマエ




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学
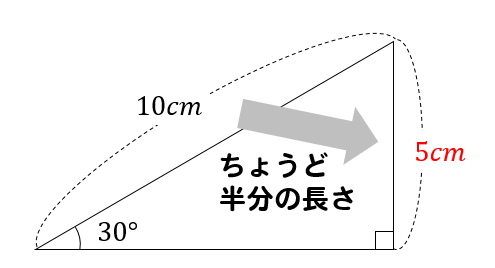



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ



世界に1つだけの三角形の組 大学院生が定理の証明に成功 数理女子
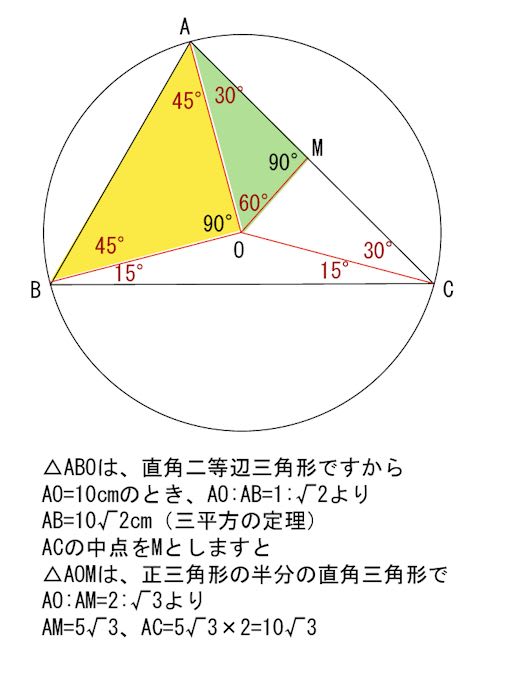



円に内接する 三角形の 問題 3 名寄 算数数学教室より



余弦定理も三平方の定理も知らない小学生でも理解できる解法はあるでしょうか Yahoo 知恵袋
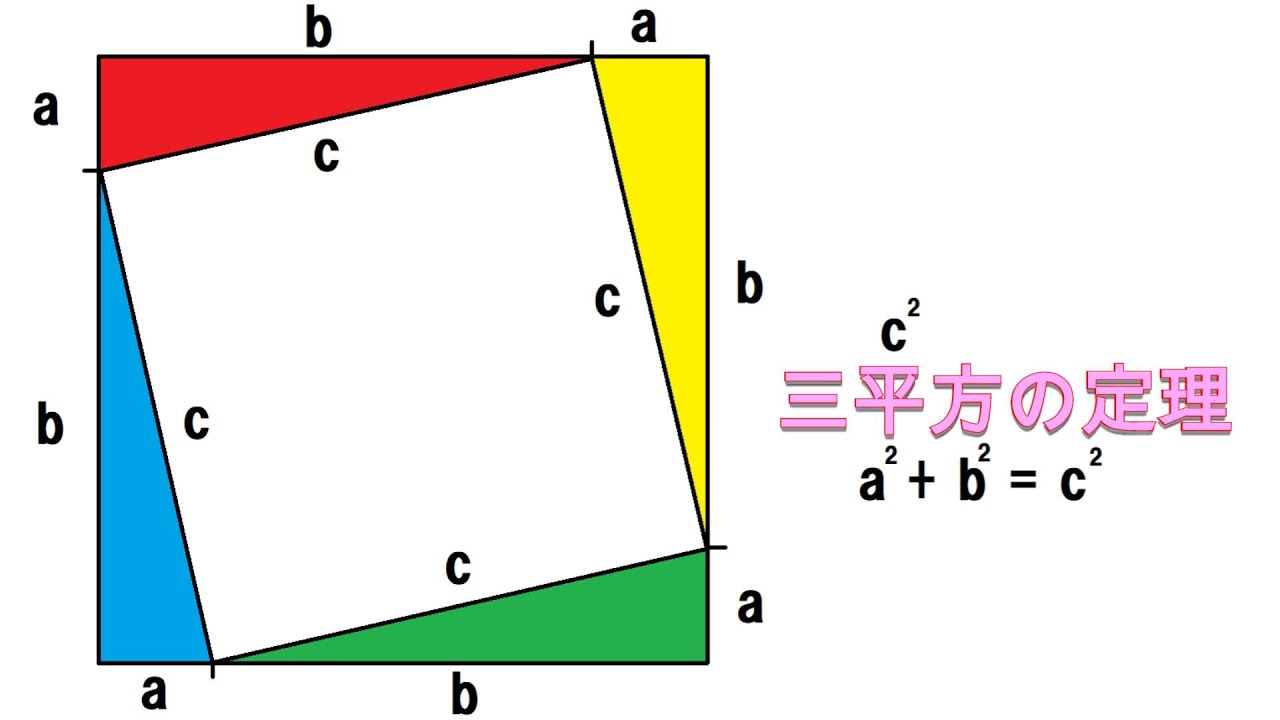



小学生でも分かる三平方の定理 Pythagoras Theorem Youtube



三平方の定理や平方根を使わずに小学生が解く方法をご教示ください Yahoo 知恵袋




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理を証明せよ 中学生課題 ふるやまんのマスラボ奮闘記




三平方の定理を使わず面積を求める が小学生向けの問題だったとはね Ts0818のブログ




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト
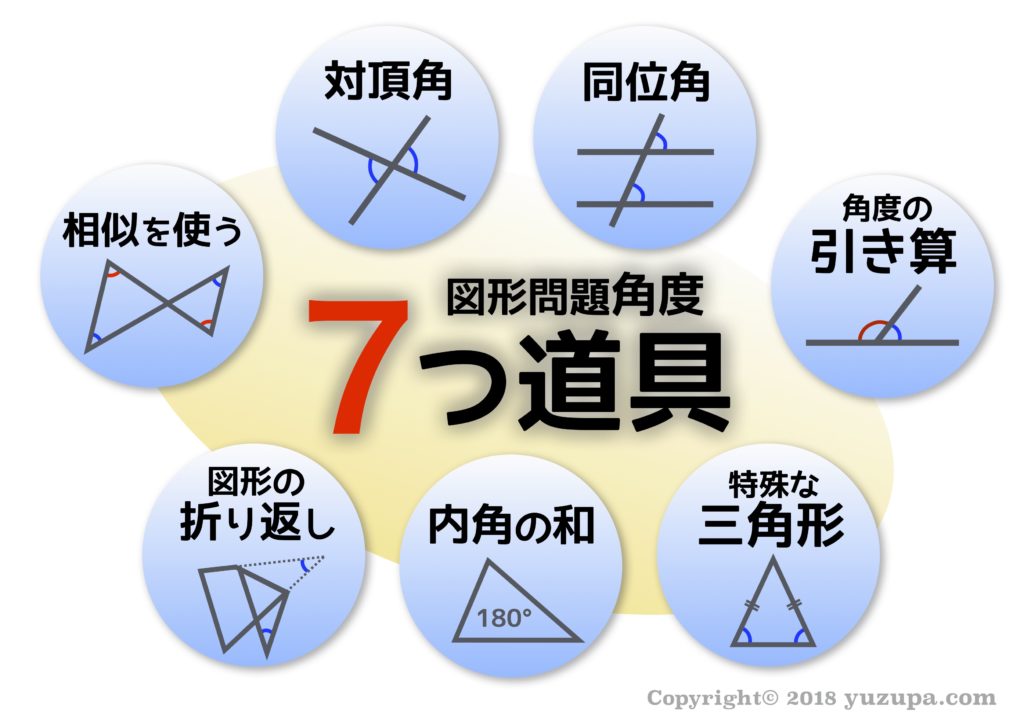



中学受験 図形の角度問題は 7つ道具 で攻略 かるび勉強部屋




直角三角形の辺を求める Youtube




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




世界一わかりやすい数学問題集中3 7章 三平方の定理




2つの直角三角形の角の和 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog



ピタゴラスの定理 の思いで チャンネルf
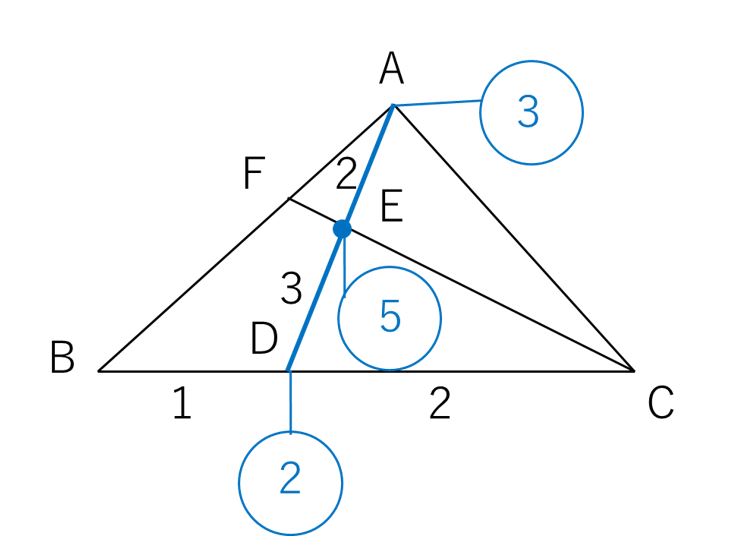



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ



質問にお答えします 小学生でもわかる数学とは 教育研究所arcs
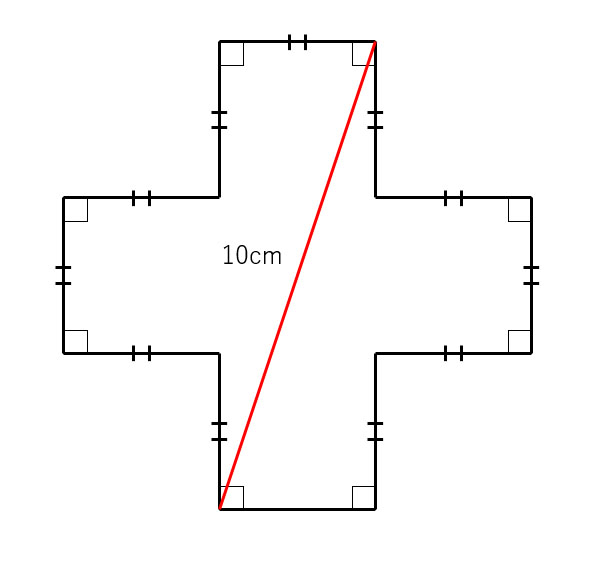



この図形の面積 三平方の定理を使わずに出せる ヒラメキで解く 算数 がちょっと手ごわい ねとらぼ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




小学生でもできるピタゴラスの定理の証明方法 算数 数学 理系思考を応援 Fireムーブメントを日本で実践するブログ
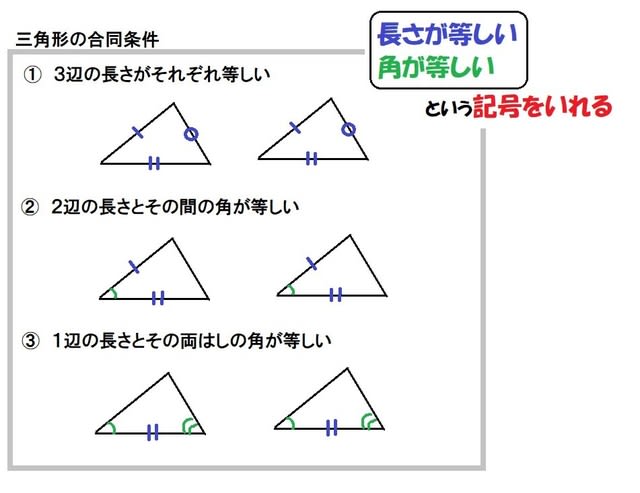



合同な図形 小5 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
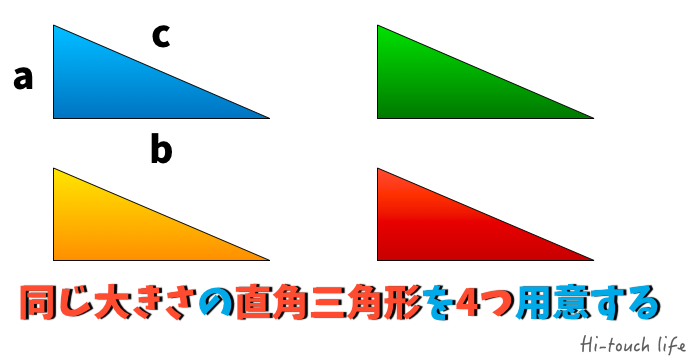



小学生でもできるピタゴラスの定理の証明方法 算数 数学 理系思考を応援 Fireムーブメントを日本で実践するブログ
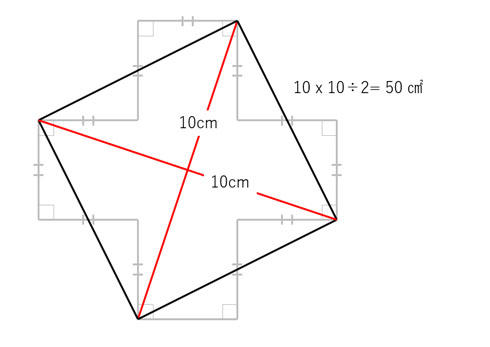



この図形の面積 三平方の定理を使わずに出せる ヒラメキで解く 算数 がちょっと手ごわい ねとらぼ



図形 角度 面積問題 三平方の定理 中学生 練習問題45 60 75 3 4 5 の三角形 みんなの算数クラブ




三角形の角度を求める問題 小学生 中学生の勉強




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導
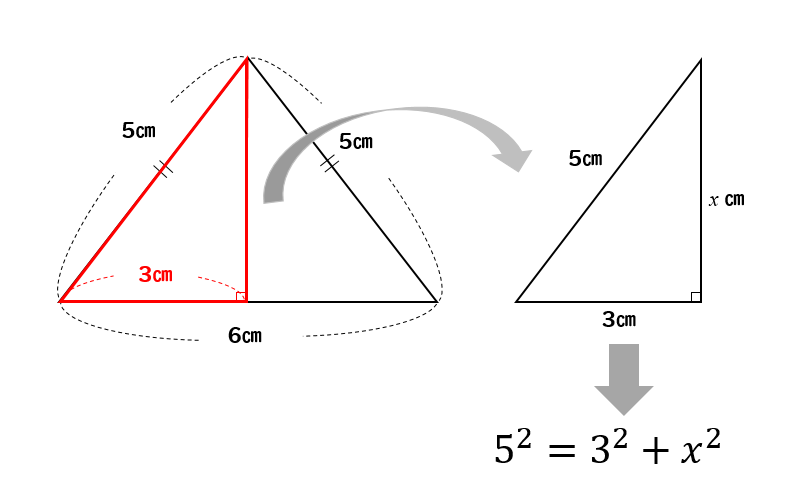



無料でダウンロード ピタゴラス の 定理 小学生
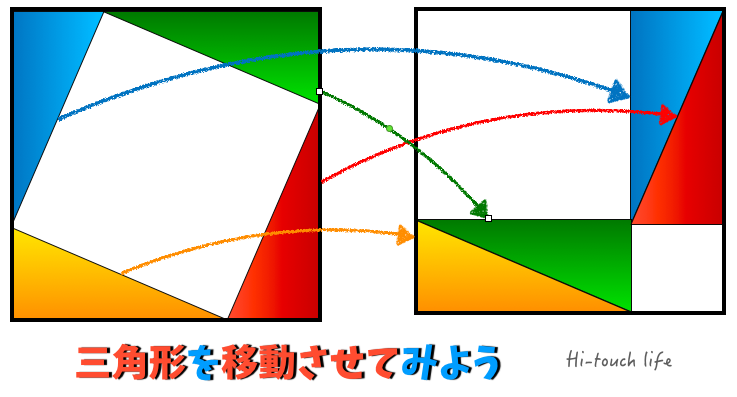



小学生でもできるピタゴラスの定理の証明方法 算数 数学 理系思考を応援 Fireムーブメントを日本で実践するブログ




新鮮なピタゴラス の 定理 小学生 子供のための最高のぬりえ




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく



図形の扉 三角形の外角の定理




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
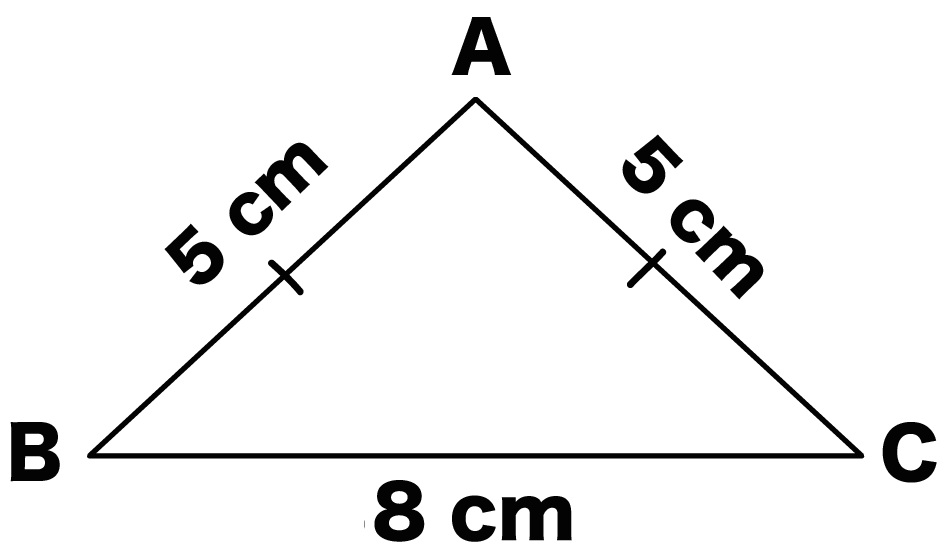



簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



面積の問題 小学生 中学生 三平方の定理 みんなの算数クラブ
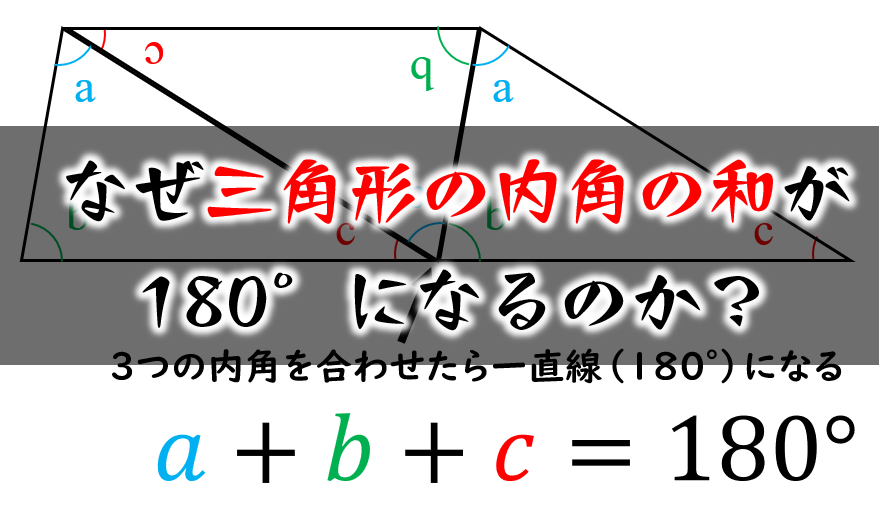



三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun
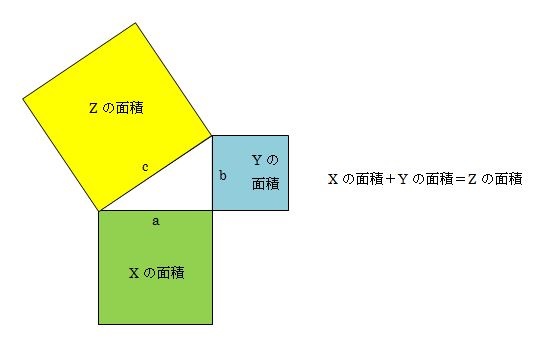



三平方の定理 もう一度やり直しの算数 数学




世界に一つだけの 三角形ペア 発見 慶大院生2人証明 朝日新聞デジタル




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




ヒポクラテスの定理は三平方の定理を知っていたら覚える必要なし 勉強法全般



1




三角形の内角の和は180度って証明できるの 三角形の外角の定理 公式 や問題アリ 遊ぶ数学
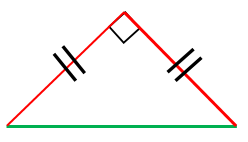



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学



三平方の定理 小学生バージョンの解き方 江戸川女子中 09年 算数解法の極意



質問にお答えします 小学生でもわかる数学とは 教育研究所arcs
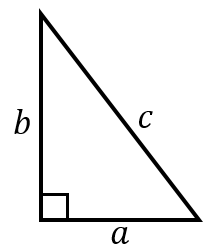



直角三角形の辺の長さの求め方と計算ツール 具体例で学ぶ数学




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




新鮮なピタゴラス の 定理 小学生 子供のための最高のぬりえ



1




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく
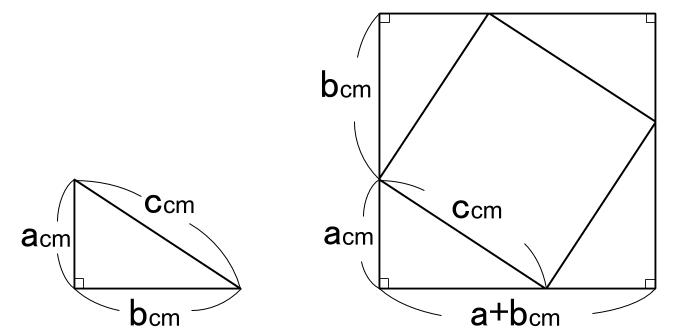



中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su




数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より




三角比 30 45 60 もう一度やり直しの算数 数学
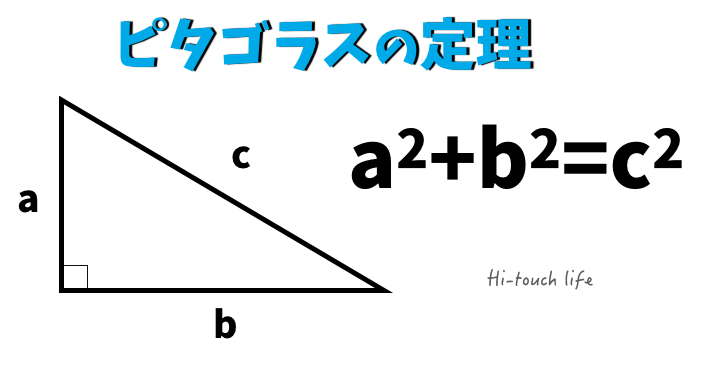



小学生でもできるピタゴラスの定理の証明方法 算数 数学 理系思考を応援 Fireムーブメントを日本で実践するブログ




タンジェントとは何か 中学生でも分かる三角関数の基礎
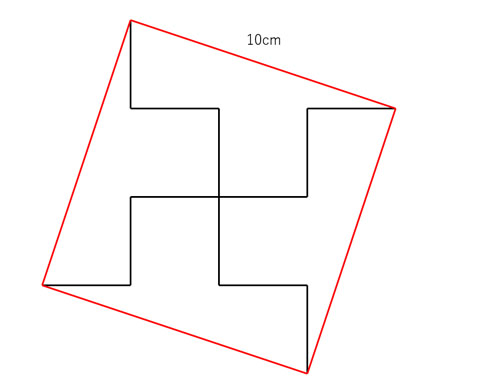



この図形の面積 三平方の定理を使わずに出せる ヒラメキで解く 算数 がちょっと手ごわい ねとらぼ
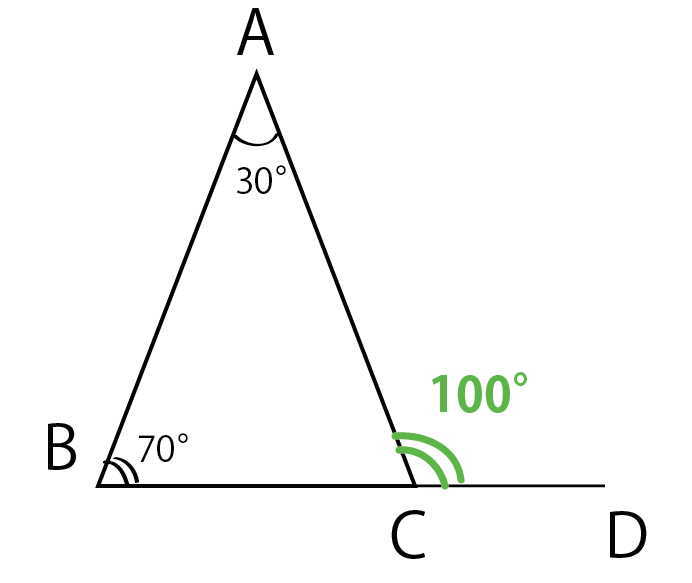



3分でわかる 三角形の外角の定理の証明 Qikeru 学びを楽しくわかりやすく




三平方の定理の4通りの美しい証明 高校数学の美しい物語



0 件のコメント:
コメントを投稿